[Algo Rhythm🕺💃] BOJ 2225 - 합분해

💫문제 분석

입력으로 주어지는 두 정수를 각각 $N,K\ (1\le N,K \le 200)$라고 하자.

그리고 0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 $f(N,K)$라고 하자.

마지막으로 N을 만들기 위해 더해지는 K개의 정수들을 순서대로 $I_1, I_2, ..., I_K$라고 하자.

 

$f(N,K)$의 규칙을 파악하기 위해 $f(2, 3)$를 구하는 과정을 분석해보자. $f(2, 3)$은 아래와 같이 6이다.

이때 $I_1$과 나머지 $I_2, I_3$의 관계를 파악해보자.

$I_1 = 0$ 일때 $I_2, I_3$를 구하는 것은 $f(2, 2)$을 구하는 것과 같다. (1이 적힌 파란 원으로 표시함)

$I_1 = 1$ 일때 $I_2, I_3$를 구하는 것은 $f(1,2)$를 구하는 것과 같다. (2가 적힌 파란 원으로 표시함)

$I_1 = 2$ 일때 $I_2, I_3$를 구하는 것은 $f(0, 2)$를 구하는 것과 같다. (3이 적힌 파란 원으로 표시함)

 

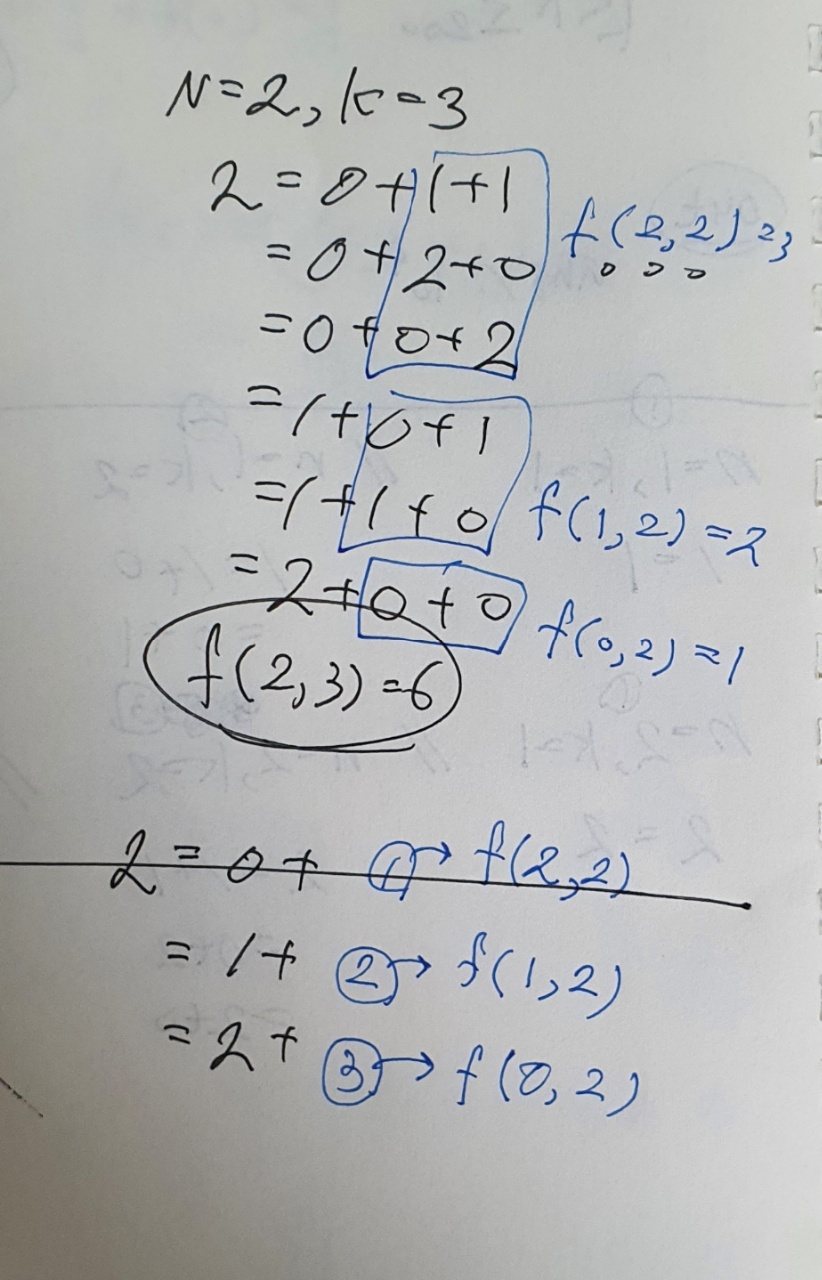
뿐만 아니라 다른 경우들을 분석하면 $N = 0$이거나 $K = 1$ 일때 $f(N, K) = 1$ 임을 알 수 있다.

이를 종합하면 $f(N, K)$는 다음과 같다는 사실을 알 수 있다.

$f(N, K)= \begin{cases} 1 & if\ N = 0\ or\ K = 1\\ \sum_{i=0}^N f(N - i, K - 1) \mod 10^9 & else \end{cases}$

 

🔥문제 풀이

$f(n, k)\ (1 \le n \le N,\ 1 \le k \le K)$를 저장하는 배열을 만든다.

그리고 bottom-up 방식으로 $f(n,k)$를 구하는데 그 때 쓰이는 점화식은 아래와 같다.

$f(N, K)= \begin{cases} 1 & if\ N = 0\ or\ K = 1\\ \sum_{i=0}^N f(N - i, K - 1) \mod 10^9 & else \end{cases}$

 

✨복잡도 분석

입력으로 두 정수 $N,K\ (1\le N,K \le 200)$이 주어질 때, 시간 복잡도와 공간 복잡도는 다음과 같다.

 

⏰시간 복잡도 : $O(N^2K)$

• bottom-up 방식으로 $f(N, K)$를 구하는데 $O(NK)$가 소모됨.
• solve 함수 실행시 $O(N)$이 소모됨.

🏠공간 복잡도 : $O(NK)$

• $f(N, K)$를 저장하기 위해 $O(NK)$가 소모됨.

 

🌈코드

 

🌏문제 출처

https://www.acmicpc.net/problem/2225

2225번: 합분해